9.1
Racket
2 Module rml-neural/activation.🔗ℹ
This module defines a set of activation functions, or method
that may be used to determine the sensitivity of neurons in a network layer.
To support both forward and backward propagation each method contains the
activation function and it’s derivative. This
Wikipedia
page has a good overview of a number of activation functions.
2.1 Activation Function Structure🔗ℹ
Contracts that encapsulate the pattern data-type or false.
Contracts used to define the procedures used in the structures below. Both
activation and derivative functions are represented as a procedure that take
a single, and return a single,
real? or
flonum?. They are
equivalent to the following contract values.
See also Parallelism with Futures
in The Racket Guide In general it
is preferable to use the flonum-activator? structure and the
corresponding flonum-activation/c form as this reduces the numeric
conversions and allows optimization such as futures to work efficiently.
This structure provides the activator function, it’s derivative, and an optional
expectation value for a given method.
f is the activation function, \phi(v_i)
df is the activation derivative function, \phi^\prime(v_i)
– sometimes shown as \phi^{-1}(v_i)
α is an optional stochastic variable sampled from a uniform
distribution at training time and fixed to the expectation value
of the distribution at test time
2.2 Activation Functions🔗ℹ
Each of the activator? structures below will be defined by it’s
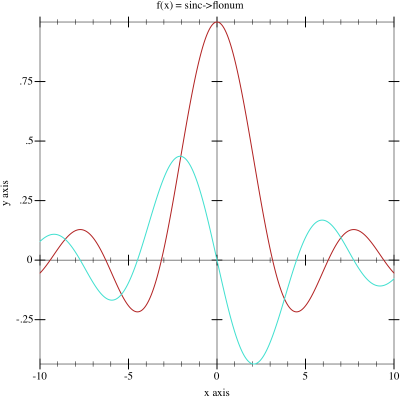
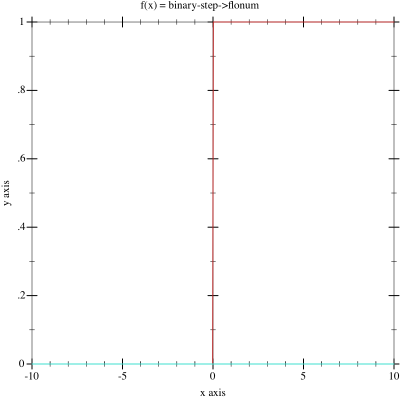
activation function (the derivative is not shown). A sample plot shows the
shape of the activation function in red and it’s derivative in turquoise.
\phi(v_i) =
\begin{cases}
0 & \text{for } v_i < 0\\
1 & \text{for } v_i \geq 0
\end{cases}
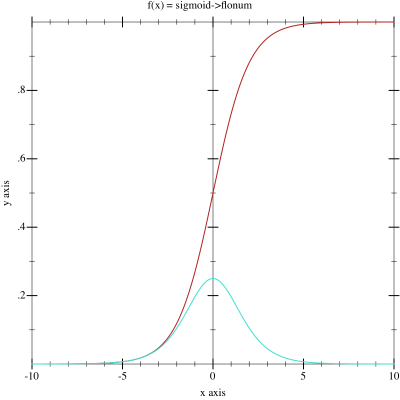
\phi(v_i) = \frac{1}{1+e^{-v_i}}
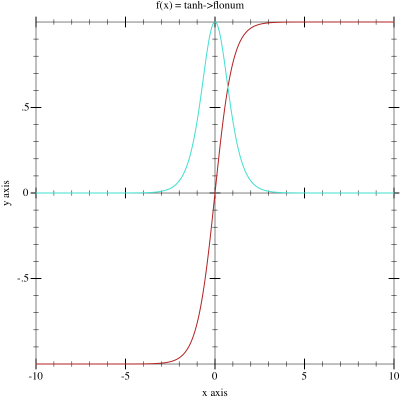
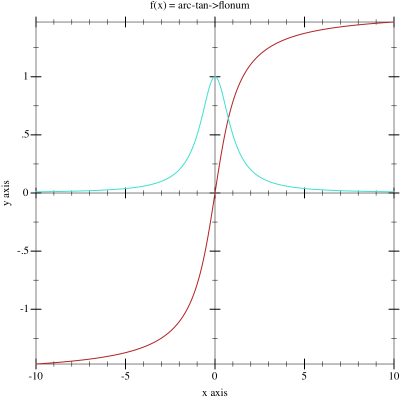
\phi(v_i) = \operatorname{atan}^{-1}(v_i)
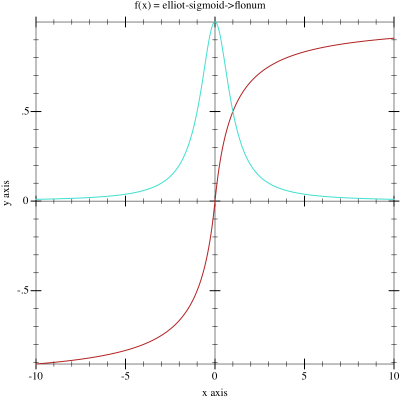
\phi(v_i) = \frac{v_i}{1+\left|v_i\right|}
\phi(v_i) = \frac{v_i}{\sqrt{1+\alpha v_{i}^2}}
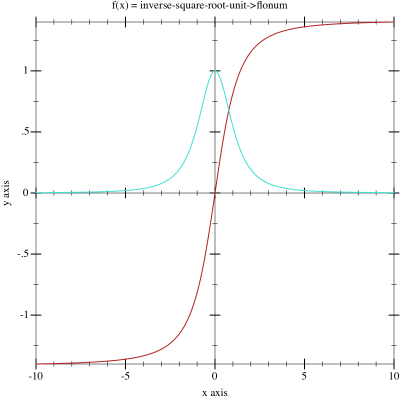
\phi(v_i) =
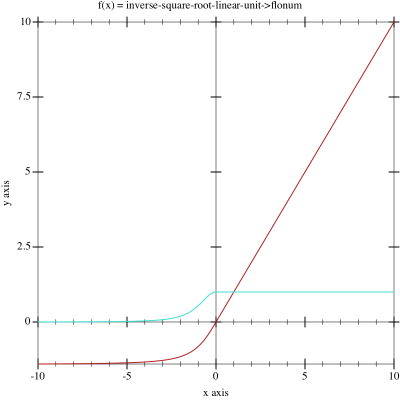
\begin{cases}
\frac{v_i}{\sqrt{1+\alpha v_{i}^2}} & \text{for } v_i < 0\\
v_i & \text{for } v_i \geq 0
\end{cases}
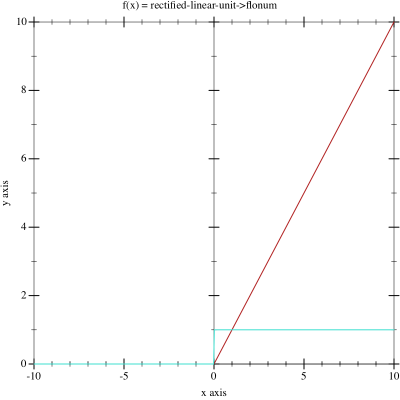
\phi(v_i) =
\begin{cases}
0 & \text{for } v_i < 0\\
v_i & \text{for } v_i \geq 0
\end{cases}
\phi(v_i) =
\begin{cases}
\delta v_i & \text{for } v_i < 0\\
v_i & \text{for } v_i \geq 0
\end{cases}
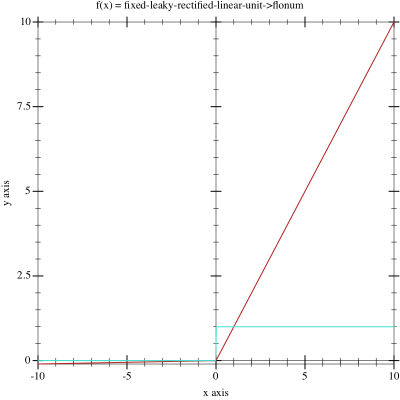
Note that the fixed form of this activator uses a delta value \delta=0.01.
\phi(v_i) = \ln\left( 1 + e^{v_i} \right)
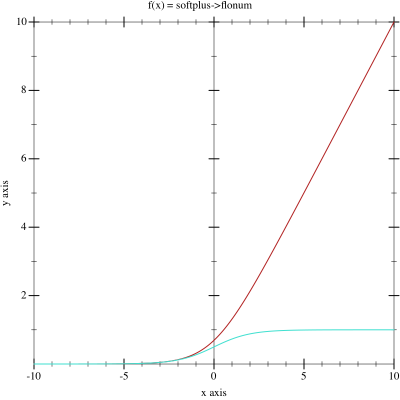
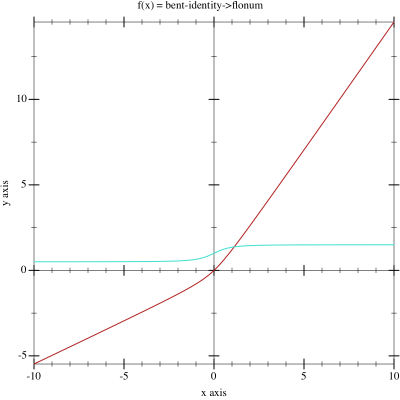
\phi(v_i) = \frac{\sqrt{v_{i}^2+1}-1}{2}+v_i
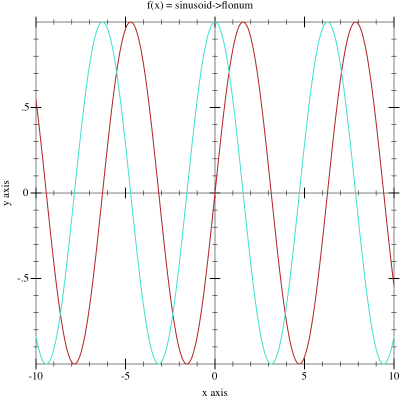
\phi(v_i) =
\begin{cases}
1 & \text{for } v_i = 1\\
\frac{\sin(v_i)}{v_i} & \text{for } v_i \neq 0
\end{cases}