4 Position and Direction Vectors
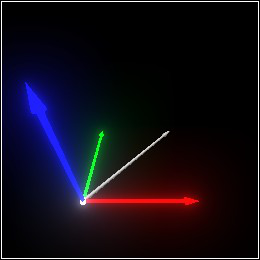
A vector in 3D space is uniquely identified by three real numbers called coordinates or components. For example, the coordinates of (pos 1 2 3) are 1, 2 and 3.
> (define dv2 (dir 0 0 1))
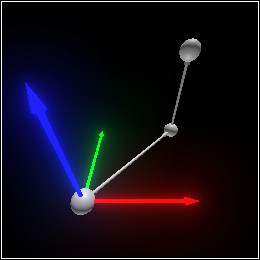
> (define move-twice (combine move-once (arrow (pos+ v dv1) dv2) (sphere (pos+ (pos+ v dv1) dv2) 0.1))) > move-twice
> (define dv (dir+ dv1 dv2))
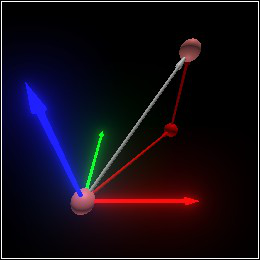
> (define move-twice-by-moving-once (combine (arrow v dv) (sphere v 0.1) (sphere (pos+ v dv) 0.1)))
> (combine move-twice-by-moving-once (set-color move-twice (rgba "red" 0.75)))
> (move (combine (with-color (rgba "red" 0.5) (cube origin 1/3)) (sphere origin 0.05)) (dir 1/2 1/2 0))
> (move (combine (with-color (rgba "red" 0.5) (rectangle origin (dir 1/3 1/3 1))) (sphere origin 0.05) (arrow origin (dir 1/3 1/3 1))) (dir 1/2 1/2 0))
4.1 Direction Vectors
procedure
v : (U FlVector (Listof Real) (Vectorof Real)) (dir dx dy dz) → Dir dx : Real dy : Real dz : Real
value
value
value
value
value
value
> (with-color (rgba "black") (combine (with-emitted (emitted "cyan" 2) (arrow origin -x)) (with-emitted (emitted "magenta" 2) (arrow origin -y)) (with-emitted (emitted "yellow" 2) (arrow origin -z))))
value
value
value
value
value
value
value
value
value
value
value
value
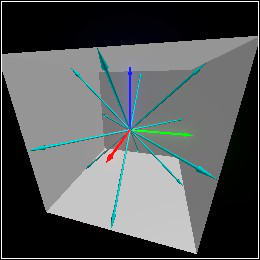
> (combine (cube origin 1 #:inside? #t) (with-color (rgba "cyan") (for/list ([dv (list +x+y +x-y +y+z +y-z +x+z +x-z -x+y -x-y -y+z -y-z -x+z -x-z)]) (arrow origin dv))) (basis 'camera (point-at (pos 2 0.5 0.75) origin)))
value
value
value
value
value
value
value
value
> (combine (cube origin 1 #:inside? #t) (with-color (rgba "magenta") (for/list ([dv (list +x+y+z +x+y-z +x-y+z +x-y-z -x+y+z -x+y-z -x-y+z -x-y-z)]) (arrow origin dv))) (basis 'camera (point-at (pos 2 0.5 0.75) origin)))
procedure
dv1 : Dir dv2 : Dir
procedure
dv : Dir s : Real
procedure
(dir-negate dv) → Dir
dv : Dir
procedure
dv1 : Dir dv2 : Dir
(dir-scale dv s) scales the direction dv by multiplying each component by s.
(dir-negate dv) returns the direction opposite dv by negating each component, and is equivalent to (dir-scale dv -1).
(dir- dv1 dv2) is equivalent to (dir+ dv1 (dir-negate dv2)).
procedure
dv : Dir p : Nonnegative-Real
procedure
(dir-normalize dv) → (U #f Dir)
dv : Dir
procedure
(dir-project dv1 dv2) → (U #f Dir)
dv1 : Dir dv2 : Dir
procedure
(dir-reject dv1 dv2 [s]) → Dir
dv1 : Dir dv2 : Dir s : Real = 1
(dir- dv1 (dir-scale (dir-project dv1 dv2) s))
procedure
(dir-reflect dv1 dv2) → Dir
dv1 : Dir dv2 : Dir
If dv is the velocity of an object that hits an immovable surface with normal n, then (dir-reject dv n) is the object’s new velocity, assuming an ideal elastic collision.
In other words, use this function to bounce things off walls in games.
procedure
(angles->dir yaw pitch) → Dir
yaw : Real pitch : Real
procedure
(dir->angles dv) → (Values Flonum Flonum)
dv : Dir
> (match-define (dir dx dy dz) (dir 1 2 3)) > (list dx dy dz) '(1.0 2.0 3.0)
4.2 Position Vectors
procedure
v : (U FlVector (Listof Real) (Vectorof Real)) (pos x y z) → Pos x : Real y : Real z : Real
procedure
(pos-between start end t) → Pos
start : Pos end : Pos t : Real
> (match-define (pos x y z) (pos 1 2 3)) > (list x y z) '(1.0 2.0 3.0)